Raspberry Pi Zero Cluster Computing Fun

Introduction

Raspberry Pis are great to learn programming and experiment around with, and Raspberry Pi Zeroes are inexpensive and small little packages that pack a decent amount of punch.

But at a single core and 512 MB of memory they may seem like they can't do that much, especially in today's world of multi-core, high speed computing, right?!

However, the adage "many hands make light work" is indeed true!

In this project, I'll show you how you can create a cluster of Raspberry Pis - using "divide and conquer", to make multiple Raspberry Pis to work together and produce results way better than a single computer can do! With parallelization, you can add even more Pis into the mix and produce even better results.

MPI or Message Passing Interface has become the defacto standard in parallel computing, and there are many implementations of it, including open source implementations like MPICH and OpenMPI.

In this project, we will

• Construct a simple two-node cluster
• Get an introduction to MPI and parallel programming
• Run some example workloads (finding all prime numbers below a certain number) to compare and contrast execution times under single-node and parallel (2-node) execution, and learn from them.

Setting up the Cluster

Case:

In this example, I'm creating a two-node cluster. I'm using ProtoStax Enclosure for Raspberry Pi Zero, that is designed to accommodate 2 Pi Zeros mounted side-by-side, as shown below.

Two-node Pi Zero Cluster with ProtoStax Enclosure for Raspberry Pi Zero

Two-node Pi Zero Cluster with ProtoStax Enclosure for Raspberry Pi Zero

It does have internal vertical clearance of 1.2 inches, plenty for a pHAT or Bonnet, so you can stack 4 Pi Zeros in there, 2 x 2. ProtoStax Enclosures are modular, consisting of different pieces that fit together to form different configurations. When stacking 4 Raspberry Pi Zeroes in there, you can leave out the long sidewalls to get access to the USB/power ports of all 4 RPis (the long sidewalls have USB/power cutouts for one Pi Zero each). See below.

Prostax Enclosure for Raspberry Pi Zero has enough vertical clearance to stack 4 RPi Zeros.

Prostax Enclosure for Raspberry Pi Zero has enough vertical clearance to stack 4 RPi Zeros.

Networking:

Cluster computers in parallel computing need to communicate with each other. That can be done via Ethernet, either wired or wireless.

In my example, I use the wireless LAN of the Raspberry Pi Zero W for cluster communications. Depending on your workload, you may need to transfer around a lot of data and have a lot of communications between the nodes - in that case, it may be more suitable to have dedicated wired connections between them that offer greater much greater throughput. You can, for example, use a Gigabit ethernet switch and have wired connections between the Raspberry Pis. In that case, you would want to switch to a more appropriate Raspberry Pi like the new 4B that also has a Gigabit Ethernet port for wired communications.

For our sample workload of prime number calculation, we don't have to worry about too much voluminous data transfer and communications, so wireless connection works just fine!

If you don't know how to prepare your Pi for wireless communications, there are many resources available on the web to help you. I have just used the basic DHCP setup with my home wireless router and configured it to give them the same IP address each time (reserved IP).

Preparing the Pis

The first thing you'll want to do is make sure that both Pis (or 4 Pis, if you're using the 4 node setup) are running the same version of the OS and are up to date. This will prevent any communications issues between different nodes using different versions of software.

I'm using the latest version of Raspbian Buster.

You'll then want to prepare the nodes to allow communications between them. One of the nodes will be a master node, and the other nodes are client (or also called slave) nodes. The master node will need communicate with every node in the cluster, and each client node needs to communicate with the master.

We'll use ssh key-based authentication.

We'll generate ssh keys using

ssh-keygen -t rsa

and then distribute the public keys to the different hosts using

ssh-copy-id <username@hostip>

The public keys need to be copied from the host to all the clients (so run the above command on

• on the host computer and specify the client ip address for each client), and
• from each client back to the host (i.e. you don't need to worry about copying them between client machines)

Then install MPI on each node (we're installing MPICH and mpi4py python bindings for MPI):

sudo apt install mpich python3-mpi4py

Testing your setup

Run this on each node

mpiexec -n 1 hostname

It will run the command hostname on that node and return the result.

Gather the IP addresses of all your nodes (see the Networking: section above) by running ifconfig.

Now run this on your master node:

mpiexec -n 2 --host <IP1,IP2>  hostname

The above command runs the hostname command on each of the nodes specified and returns the results.

If you've gotten this far, ok, all set! You're good to go!

A Bird's Eye Look at Parallel Computing

Here is a brief overview of parallel computing and what it is all about. This is just scratching the surface - a 30, 000 ft from an airplane, rather than a bird's eye view, if you may!

There are many ways in which you can utilize the RPi Cluster you have just created, or even squeeze more juice out of a single Raspberry Pi. You can use concurrency techniques like multi-threading to be able provide the illusion of parallel execution - utilizing the CPU by one thread, while another thread may be waiting on some IO, for example, and time-slicing between the different threads. If you have a multi-core processor, like on a Raspberry Pi 4B, you can actually run multiple processes in parallel and get real parallelism. With the aid of communications paradigms like MPI, you can run multiple processes on different physical nodes and coordinate between them, to get parallelism beyond a single node (and even on a single node). In this example, we utilize MPI to parallelize finding prime numbers below a certain number (for example, all primes below 100 million!).

To be able to harness the power of parallel computing, you need to be able to decompose the given problem into a bunch of tasks, one or more of whom can be performed in parallel. Each task should be able to run in parallel and independently. After that, there's some communications and consolidation of results that can take place, to produce the final result.

MPI offers communication paradigms to help decompose, run the tasks, communicate, and collect the results.

Let's take a look at an example to understand the concepts - finding prime numbers. But first, let's get a very brief introduction to MPI.

A Brief Introduction to MPI

A tutorial on MPI would take up far more space than can be devoted here, so I'm not even going to try. However, I would like to give you just a brief taste/view of an MPI program - a "Hello World" or "Blinking LED" equivalent - hopefully that will stimulate your appetite and make you interested for more!

In C, you start off with MPI_Init to initialize the inter-process communcations, and at the end, you call MPI_Finalize(). In between, you can do the work of running the tasks of your parallel algorithm, and can use MPI constructs like size (number of nodes in the cluster), rank (where you are in the cluster, and it can act as your ID within the cluster), and name (gives you the name of the node).

#include <mpi.h> 
#include <stdio.h>

int main(int argc, char *argv[]) 
{    
   int size, rank, len;  
   char name[MPI_MAX_PROCESSOR_NAME];
#if defined(MPI_VERSION) && (MPI_VERSION >= 2)    
   int provided;    
   MPI_Init_thread(&argc, &argv, MPI_THREAD_MULTIPLE, &provided);
#else    
   MPI_Init(&argc, &argv);
#endif    
   MPI_Comm_size(MPI_COMM_WORLD, &size);    
   MPI_Comm_rank(MPI_COMM_WORLD, &rank);    
   MPI_Get_processor_name(name, &len);    
   printf("Hello, World! I am process %d of %d on %s.n", rank, size, name); 
   MPI_Finalize();    
   return 0;
}

The same code in Python is a little shorter, because the bindings take care of some of it.

#!/usr/bin/env python
"""Parallel Hello World"""
from mpi4py import MPI
import sys
size = MPI.COMM_WORLD.Get_size()
rank = MPI.COMM_WORLD.Get_rank()
name = MPI.Get_processor_name()
sys.stdout.write(
    "Hello, World! I am process %d of %d on %s.n"
    % (rank, size, name))

Here is the sample output that I got:

$ mpiexec -n 2 --host 10.0.0.98,10.0.0.162 python3 mpihelloworld.py

Hello, World! I am process 0 of 2 on proto0.
Hello, World! I am process 1 of 2 on proto1.

Ok, how do we go from there to running some task/algorithm in parallel? Read on!

Computing Prime Numbers

First, a quick recap of what a prime number is. It is a number that is divisible only by itself and 1, and no other number. Numbers 2, 3, 5, 7, 11, 13 are all examples of prime numbers.

Prime numbers and their interesting properties are useful in modern cryptography, and if you are interested in how they are used, I've included a reference at the end for your reading pleasure! Shortly put, modern encryption algorithms utilize math-level security - that we can easily take two large primes and multiply them to get a very large number, but it is a much harder problem to take a really large number and find out which two primes went into making it. Computing primes up to a large number is fun, but as you can see, has some practical aspects to it as well!

The problem we are trying to solve is to find all prime numbers that are less than a given number - For example, all primes less than 20 are

2, 3, 5, 7, 11, 13, 17 and 19.

How about all primes that are less than 10, 000? Or all primes less than 1, 000, 000? Clearly, hand calculation is not going to work, and we're going to have to resort to computing power.

The Brute Force Way

You can find out if a number N is a prime by dividing it by all numbers from 2 to N-1, and see if the remainder is zero (0). If none of the results are 0, then the number is a prime.

To find all primes between a starting and ending range, test each number in the range to see if it a prime (as described above). Keep a note of such primes discovered.

Ok, how about the parallel algorithm that I was talking about? How does that work here?

In the parallel algorithm for this brute force way, it becomes easy to be able to divvy up the task and decompose it.

Each node takes half the numbers in the given range (say 1000) and test each number in that range to see if it is a prime, and returns the results. One node tries to find primes between 2 and 500, and the other node tries to find primes between 501 and 1000.

The master node then does the additional work of putting together the results returned by the individual nodes and presenting the consolidated information to the user.

Using MPI, each node can find out its rank the in the cluster, and can then use that information to figure out which range of numbers that it is going to work with.

In the prime.py example that I'm using, the divvying up is done slightly differently, but the idea is the same:

# Number to start on, based on the node's rank
start_number = (my_rank * 2) + 1
for candidate_number in range(start_number,end_number, cluster_size * 2):

The rank is 0 or 1 (since we have 2 nodes). start_number is therefore either 1 or 3. Since the cluster size is 2, we step over by 4. The result is that all multiples of 2 get removed (i.e. not processed), which is a little better than testing multiples of 2, and is therefore a slight improvement over the absolute worst brute force approach. In this approach, in a 1000 numbers, each node processes about 250 numbers.

The master node gathers the prime number arrays from each node and then consolidates them and gives the results.

If we run this as a cluster of one, that is in effect the same as running it on a single node as a non-parallel algorithm.

mpiexec -n 1 python3 prime.py <N>

Running it on two nodes is as follows:

mpiexec -n 2 --host <IP1,IP2> python3 prime.py <N>

where N is the number up to which we want to compute primes.

Results

I ran the experiment with computing primes up to 1000 (N=1000), all the way to N=100, 000, in increments of 10, 000, both on a single node and on 2 nodes, and plotted the data.

To find all primes below 100, 000, a single RPi Zero took 2939 seconds or almost 49 minutes, while a 2 node cluster took 1341 seconds or a little over 22 minutes - a little better than twice as fast!

Thus you can see that as the number grew, running the task in parallel certainly paid off! If you make a 4 node cluster (which still takes about the same amount of space physically in the ProtoStax Enclosure for Raspberry Pi Zero), you can get better than 4 times as fast!

Computing Primes on 1 node vs 2 nodes

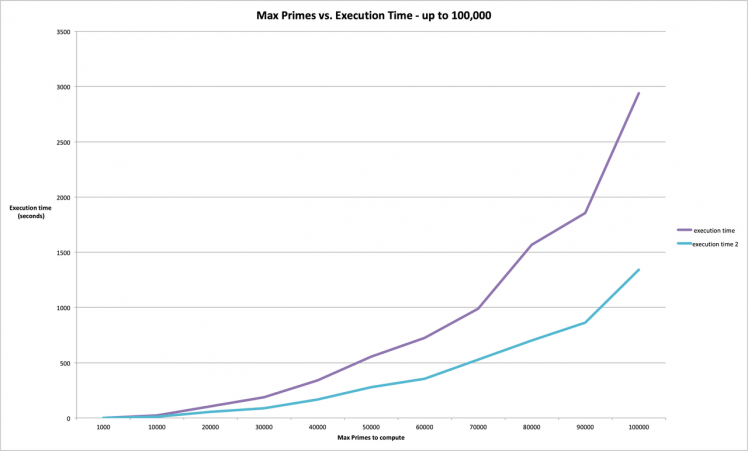
Computing Primes on 1 node vs 2 nodes

But, can we do better? We are, after all, using a brute force approach in testing for a prime. Let's look at an alternate algorithm for computing prime numbers up to N, and then look at how we can run that algorithm in parallel - hopefully, that will help you understand some of the concepts of parallel algorithms a bit more. I'm keeping it as simple as I can, I promise!

The Sieve of Eratosthenes

The Sieve of Eratosthenes is an ingenious and ancient algorithm for finding primes up to a given number.

It does so by marking as composite numbers (i.e. non-primes) those numbers that are multiples of a primes. Let's start with a simple example of finding all primes less than or equal to 30.

We start with 2, which is a prime. We can then eliminate 4, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30 as composite numbers right away, because they are all multiples of 2!

The next number in the sequence is 3, which is a prime. We can similarly eliminate 6, 9, 15, 21, 27 as non-primes.

The next number in the sequence that has not been eliminated yet is 5, which is therefore a prime. We can eliminate 25 as a non-prime. (10, 15, 20 and 30 were already eliminated earlier as we have seen).

The next number in the sequence that has not been eliminated is 7, which is a prime. We then eliminate multiples of 7 - 14, 21, 28 should be eliminated (and have already been eliminated earlier).

The next number in the sequence not eliminated yet is 11, which is a prime. Its multiple 22 has already been removed.

The next up is 13, which is a prime. Its multiple is 26, which is not a prime - but it has already been eliminated.

The next number in the sequence not eliminated is 17, which is a prime. Its multiple is higher than 30, so there is nothing to eliminate. Similarly, 19, 23, and 29 remain.

You get the idea. The final result is

2, 3, 5, 7, 11, 13, 17, 19, 23, 29

or 10 primes that are less than 30.

The Sieve of Eratosthenes and Parallel Computing

Adapting an algorithm for parallel computing can be a little tricky. The key is to break it down to steps, and identify which of those can be run in parallel. The point to note is that all the steps may not be able to be parallelized.

At first glance, it doesn't look like the Sieve of Eratosthenes algorithm lends itself well to parallelizing. You need to start from the lowest number and start eliminating up, to find out the next prime!

For this, we utilize a fascinating property of the Sieve of Eratosthenes algorithm. You notice in the algorithm explanation above that after a while, all the non-primes have already been eliminated by the previous steps. By the time you reach the prime less than or equal to square-root of N (aka sqrt(N)), you have already eliminated all the non-primes in the whole list!

Since this is a 30, 000 ft view of the algorithm, I'll leave it at that, but have included resources below that will give you a whole lot more information - but I think the above overview will help you as you delve into the details.

What this boils down to is that each node in the cluster must compute the primes from 2 to square-root of N. After that, they can divvy up the remaining batch of numbers, and use their primes in (2 to sqrt(N)) list to start marking off non-primes in their batch of numbers - each node gets 1/M of the remaining numbers, where M is the size of the cluster (2 in our case). The numbers that are not eliminated are all primes!

Once they have done that, they send their smaller list back to the master node, which then uses those to construct the master list of primes.

So, is this parallelization worth it, for an already faster algorithm? After all, each node must compute all primes from 2 to sqrt(N)! Let's see below! 😊

Results

At first glance, it appears that there isn't much of a difference between running the Sieve of Eratosthenes algorithm on one node or two nodes - they are so blazingly fast that the extra work to farm out the algorithm to two nodes, and then consolidating the information, etc, doesn't really make any difference. For primes below 100, 000, the execution time is almost nothing, compared to the brute force algorithm!

The execution times for 100, 000 are

1 node = 0.003854 seconds (Sieve of Eratosthenes)

2 nodes = 0.006789 seconds (Sieve of Eratosthenes)

1 node = 2939.28 seconds (Brute Force)

2 node = 1341.25 (Brute Force)

In fact, it takes a little longer to run it on two nodes that on one node (though they are essentially almost nothing!) From the graph below, you can see execution times for Sieve of Eratosthenes, whether one node or two node, to be almost zero in comparison to the rest of the results!

Computing Primes - One Node vs. Two Nodes and Brute Force vs. Sieve of Eratosthenes

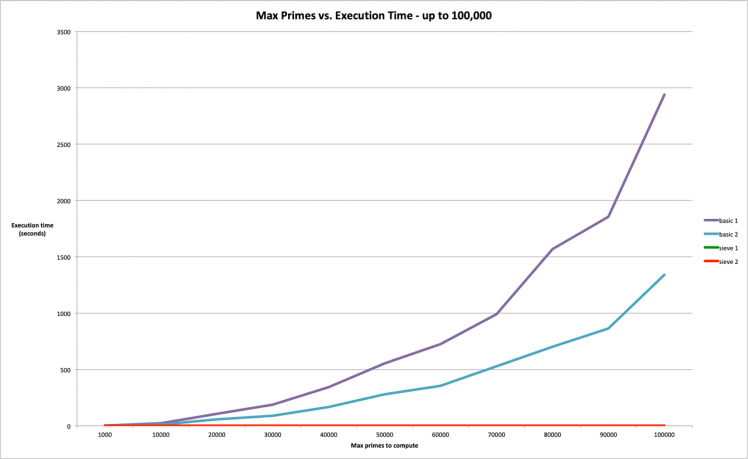
Computing Primes - One Node vs. Two Nodes and Brute Force vs. Sieve of Eratosthenes

Since our algorithm scales so well, let's ramp it up! Why stop with 100, 000? We can go much higher, it seems! I ran experiments all the way up to 100 million - that's where you start seeing the difference of parallelization! Running Sieve of Eratosthenes on two nodes starts making a real difference!

The graph of execution times of the Sieve of Eratosthenes on one node and two nodes are shown below, from 10 million (= 0.943648 seconds on one node, 0.318890 on two nodes) to 100 million (= 103.308105 seconds on one node, 24.704637 on two nodes)

So we can see that the parallelization of the algorithm is even better than a two-fold speedup as was seen in the brute force algorithm (where you're basically just divvying up the set of numbers by 2, and brute forcing each number to find out if it is a prime or not).

So even though both nodes have to compute the all primes (by Sieving) from 2 to sqrt(N) - the part that has to be serialized - the knocking off of non-primes on the remaining numbers happens very fast when done in parallel.

Computing Primes - Sieve of Eratosthenes Parallelized - One Node vs. Two Nodes

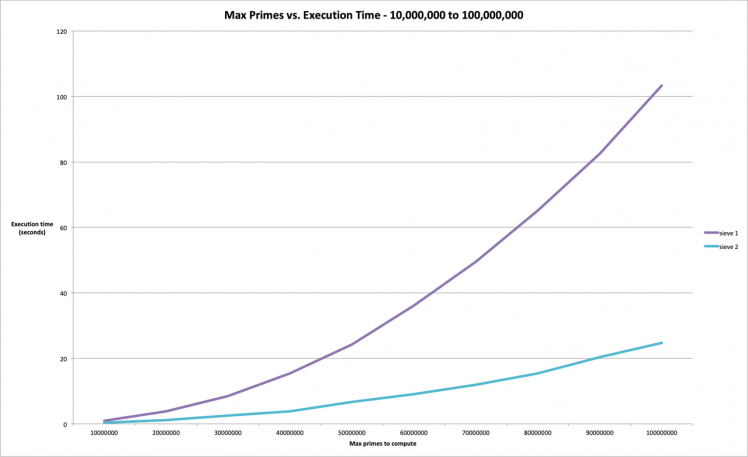
Computing Primes - Sieve of Eratosthenes Parallelized - One Node vs. Two Nodes

With a humble two-node Raspberry Pi Zero cluster, we were able to find all primes below 100 million in about 24 seconds! I really can't wait for you to tell me how fast it is for a 4-node cluster! 😊

Conclusion

In this project, we have learnt how to set up a Raspberry Pi Cluster with MPI, and also learnt about some of the high level fundamentals of parallel computing, MPI, and algorithms for computing prime numbers below a given (large) number, and how to think about parallelizing such algorithms.

At the end, we have an impressive number crunching machine that can compute all primes below 100 million in less than 24 seconds!

Taking It Further

Hopefully, this has interested you to try your hand at Cluster computing and play around with MPI and parallel computing! Here are some things that you can do to take this project further and give it wings!

• Build a 4 node cluster
• See how long it takes to compute primes on a 4 node cluster, and see how high you can go!
• Learn more about MPI
• Look at other parallel algorithm examples. Write a program to compute Pi to the Nth decimal place in parallel - Pi computing Pi - how appropriate! 😊

Can you think of any more? Write a comment below to let us know! 😊 Feel free to also ask any questions you may have! 😊

Happy making! 😊